Question 1 :

Quelle est l'asymptote horizontale de la fonction \( f(x) = \frac{2x+3}{x+5} \) ?

Question 2 :

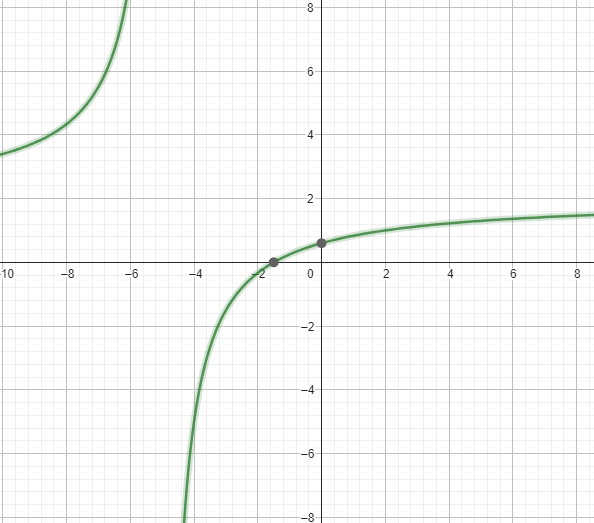
Soit \( f(x) = \frac{1}{x-2} \). Quelle est l'asymptote verticale de cette fonction ?

Question 3 :

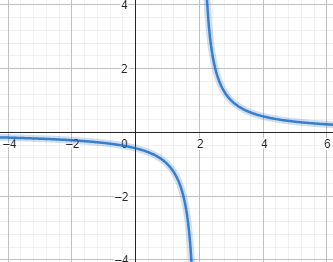
Quelle est l'asymptote horizontale de la fonction \( f(x) = \frac{5x^2+3}{2x^2+1} \) ?

Question 4 :

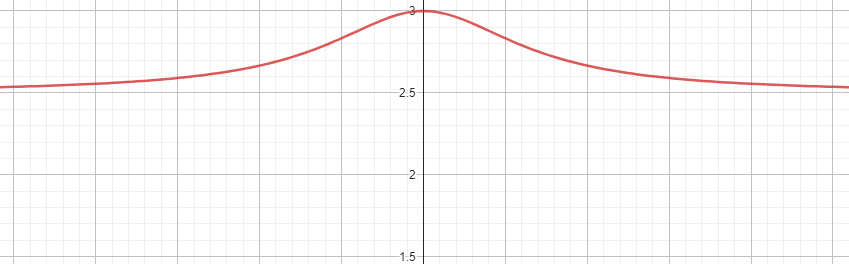
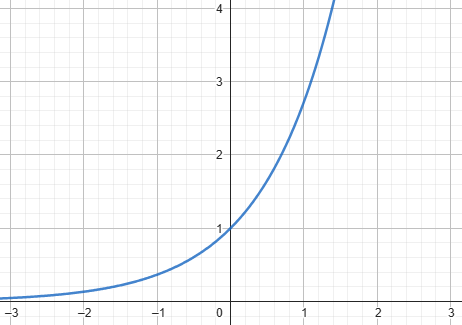
Soit \( f(x) = e^x \). Existe-t-il une asymptote horizontale lorsque \( x \) tend vers \( -\infty \) ?

Question 5 :

Soit \( f(x) = \frac{x^2+1}{x-3} \). Quelle est l'asymptote verticale de cette fonction ?

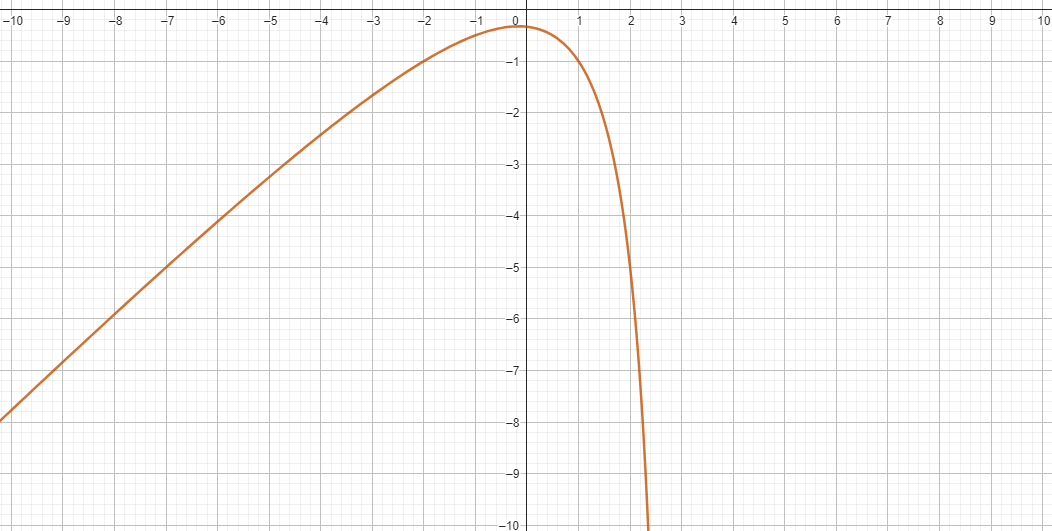
Question 6 :

Quelle est l'asymptote oblique de la fonction \( f(x) = \frac{x^2+x+1}{x} \) lorsque \( x \) tend vers \( +\infty \) ?

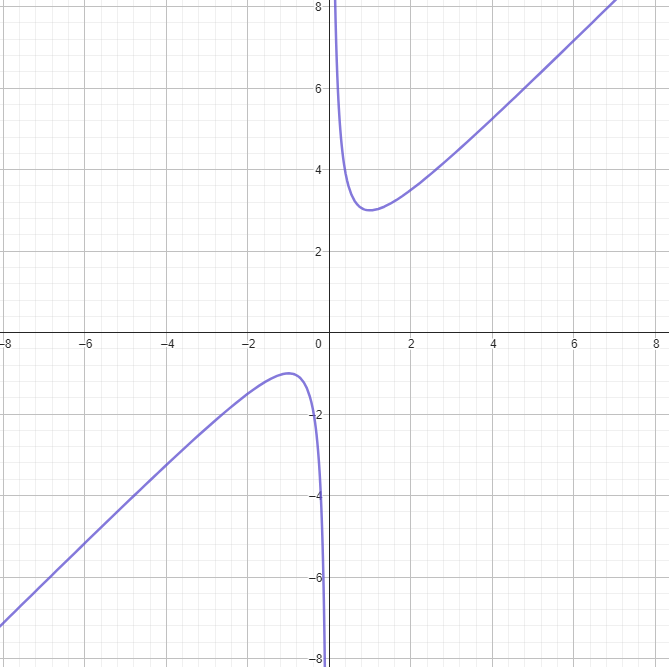
Question 7 :

Soit \( f(x) = \frac{3x^2+1}{x+4} \). Quelle est l'asymptote oblique de cette fonction lorsque \( x \) tend vers \( +\infty \) ?

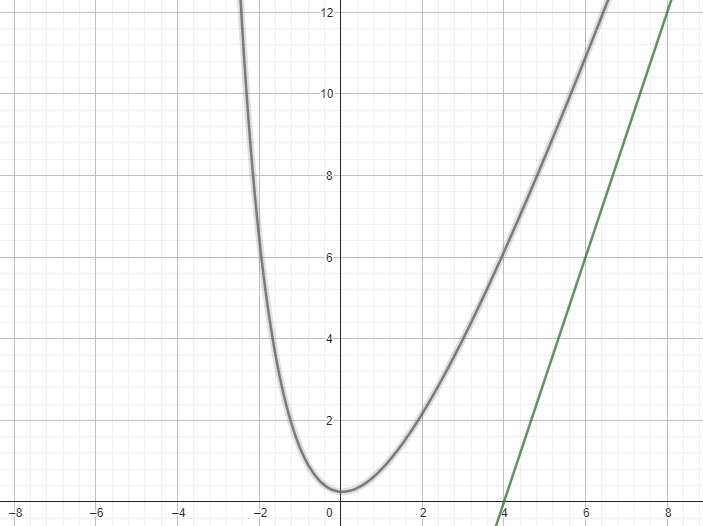
Question 8 :

Soit \( f(x) = \frac{2x^3 + 3x^2 + 1}{x^2 - 4} \). Quelle est l'asymptote verticale ?

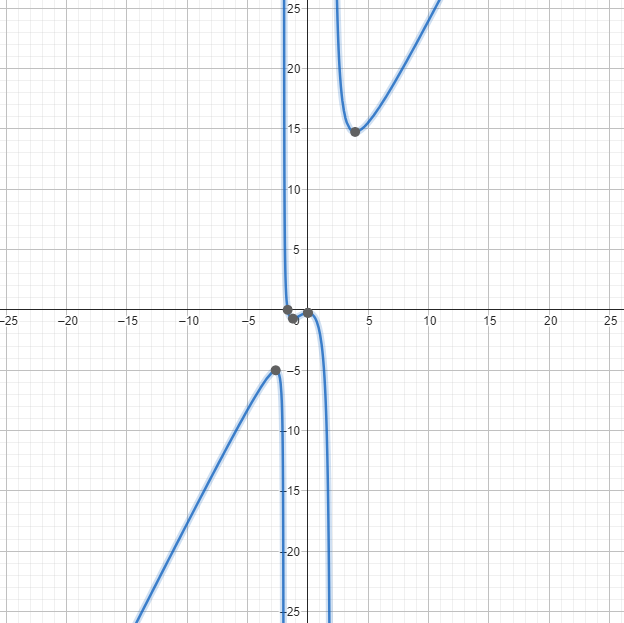
Question 9 :

Quelle est l'asymptote horizontale de la fonction \( f(x) = \frac{4x + 2}{x - 3} \) ?

Question 10 :

Soit \( f(x) = \frac{2x^2 + 3}{x^2 + 1} \). Quelle est l'asymptote horizontale de cette fonction ?

Déterminer l'asymptote horizontale de la fonction :

\( f(x) = \frac{3x^2 + 2x - 1}{x^2 - 4} \)

L'asymptote horizontale est y =

Trouver l'équation de l'asymptote oblique de la fonction :

\( g(x) = \frac{2x^2 + 3x - 1}{x + 2} \)

L'asymptote oblique est de la forme y = ax + b

a = , b =

Identifier l'asymptote verticale de la fonction :

\( h(x) = \frac{x^2 + 1}{x - 3} \)

L'asymptote verticale est x =

Déterminer les asymptotes de la fonction exponentielle :

\( f(x) = e^x \)

Asymptote horizontale : y =

Identifier les asymptotes de la fonction logarithmique :

\( g(x) = \ln(x) \)

Asymptote verticale : x =