Thèmes de Mathématiques

Question 1 :

Soit la fonction \(f(x) = 3x + 2\). Cette fonction est-elle continue sur \(\mathbb{R}\) ?

a) Oui, elle est continue sur \(\:\) \(\mathbb{R}\) b) Non, elle n'est pas continue c) Oui, mais seulement sur \(\:\) \([0, +\infty[\) d) Non, elle est continue seulement en \(\:\) \(x = 0\)

Question 2 :

Soit la fonction \(f(x) = \frac{1}{x}\). En quel point cette fonction est-elle discontinue ?

a) En \(\:\) \(x = 1\) b) En \(\:\) \(x = 0\) c) En \(\:\) \(x = -1\) d) En \(\:\) \(x = \infty\)

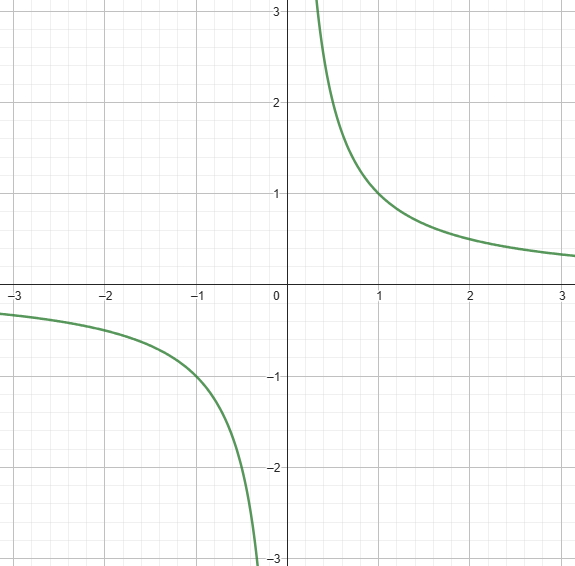
Question 3 :

Soit la fonction \(f(x) = \ln(x)\). La fonction est-elle continue sur \(\mathbb{R}\) ?

a) Oui, sur tout \(\;\) \(\mathbb{R}\) b) Non, elle est discontinue en \(\;\) \(x = 0\) c) Non, elle est continue uniquement sur \(\;\) \(]0, +\infty[\) d) Non, elle est discontinue en \(\;\) \(x = 1\)

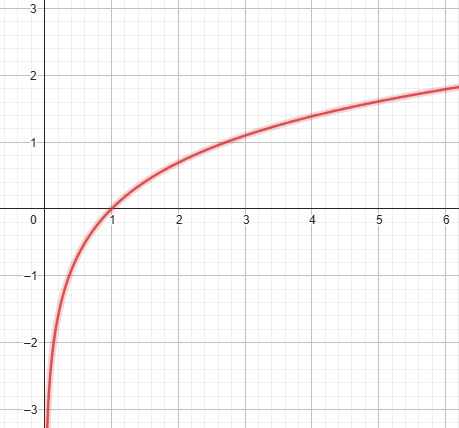
Question 4 :

Si une fonction admet un saut en \(x = a\), quel type de discontinuité a-t-elle en ce point ?

a) Discontinuité essentielle b) Discontinuité de première espèce c) Discontinuité de seconde espèce d) Pas de discontinuité

Question 5 :

La fonction \(f(x) = \begin{cases} x^2 & \text{si } x \neq 1 \\ 3 & \text{si } x = 1 \end{cases}\) est-elle continue en \(x = 1\) ?

a) Oui, elle est continue en \(\;\) \(x = 1\) b) Non, elle a une discontinuité de première espèce en \(\;\) \(x = 1\) c) Non, elle a une discontinuité essentielle en \(\;\) \(x = 1\) d) Non, elle est discontinue en tout point

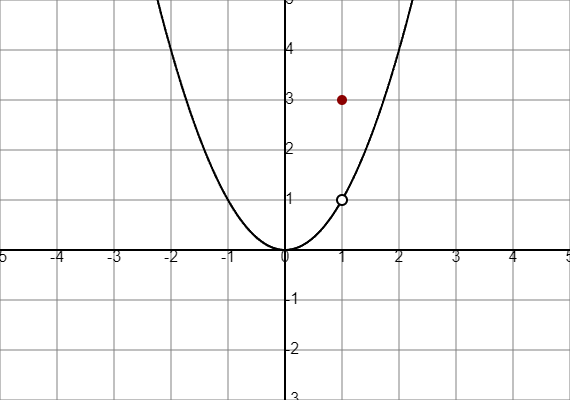
Question 6 :

La fonction \(f(x) = \frac{x^2-1}{x-1}\) est-elle continue en \(x = 1\) ?

a) Oui, elle est continue en \(\;\) \(x = 1\) b) Non, elle est discontinue en \(\;\) \(x = 1\) c) Oui, après simplification d) Non, elle est continue uniquement en \(\;\) \(x = 0\)

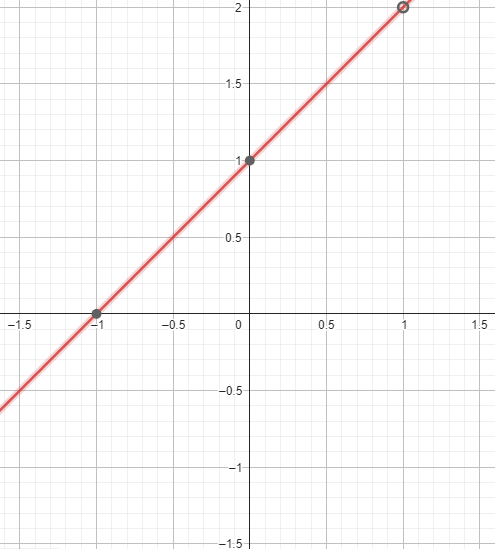
Question 7 :

Soit \(f(x) = |x|\). Cette fonction est-elle continue en \(x = 0\) ?

a) Oui, elle est continue en \(\;\) \(x = 0\) b) Non, elle est discontinue en \(\;\) \(x = 0\) c) Oui, mais seulement sur \(\;\) \([0, +\infty[\) d) Non, elle est continue uniquement sur \(\;\) \(\mathbb{R}^*\)

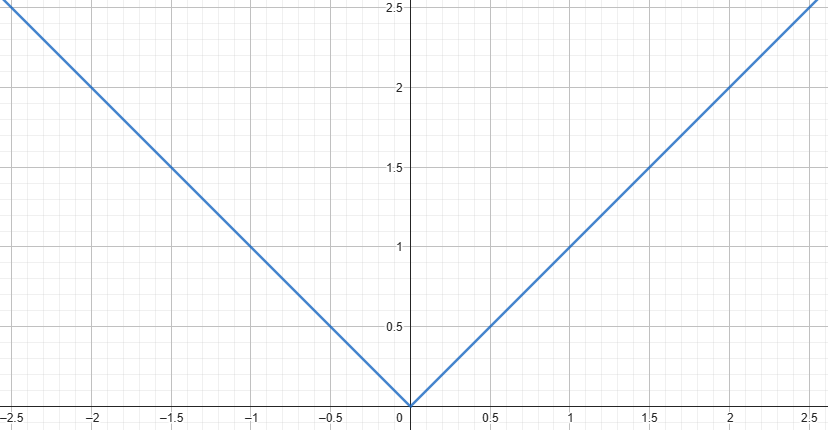
Question 8 :

Soit la fonction \(f(x) = \frac{1}{x^2}\). Est-elle continue en \(x = 0\) ?

a) Oui, elle est continue en \(\;\) \(x = 0\) b) Non, elle a une discontinuité de première espèce en \(\;\) \(x = 0\) c) Non, elle a une discontinuité essentielle en \(\;\) \(x = 0\) d) Non, elle est continue uniquement sur \(\;\) \(\mathbb{R}^*\)

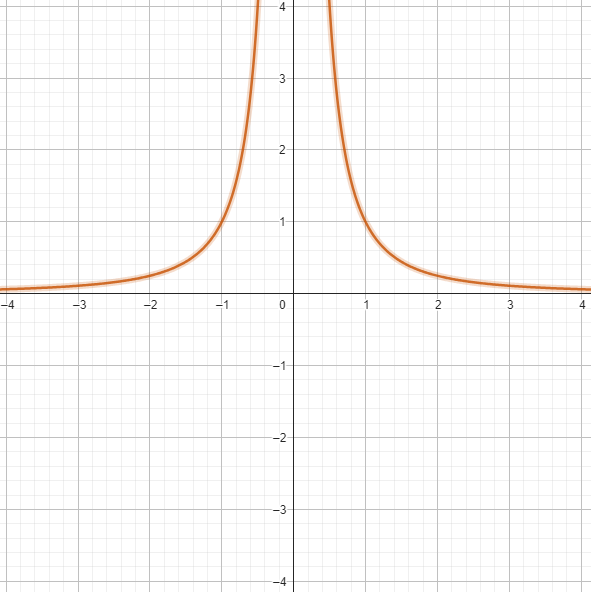
Question 9 :

Si une fonction est continue sur un intervalle fermé et borné, que peut-on dire de son image ?

a) Son image est un intervalle fermé et borné b) Son image est un intervalle ouvert c) Son image n'est pas bornée d) Son image est un intervalle semi-ouvert

Question 10 :

Soit \(f(x) = \frac{1}{x-2}\). Quelle est la nature de la discontinuité en \(x = 2\) ?

a) Discontinuité de première espèce b) Discontinuité de seconde espèce c) Discontinuité essentielle d) Pas de discontinuité

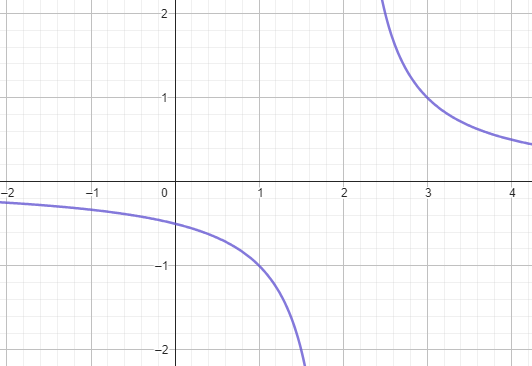
Déterminer si la fonction suivante est continue en x = 2 :

\( f(x) = \begin{cases} x^2 - 4 & \text{si } x < 2 \\ 2x - 2 & \text{si } x \geq 2 \end{cases} \)

La fonction est-elle continue en x = 2 ?

Explication: Pour que la fonction soit continue en x = 2, les limites à gauche et à droite doivent être égales à f(2). Ici, \( \lim_{x \to 2^-} f(x) = 0 \), \( \lim_{x \to 2^+} f(x) = 2 \), et f(2) = 2. La fonction n'est donc pas continue en x = 2.

Trouver la valeur de k pour que la fonction soit continue en x = 1 :

\( g(x) = \begin{cases} x^2 + 1 & \text{si } x < 1 \\ kx + 2 & \text{si } x \geq 1 \end{cases} \)

k =

Explication: Pour que la fonction soit continue en x = 1, on doit avoir \( \lim_{x \to 1^-} g(x) = \lim_{x \to 1^+} g(x) = g(1) \). Donc, 1^2 + 1 = k(1) + 2, ce qui donne k = 0.

La fonction suivante est-elle continue sur tout son domaine de définition ?

\( h(x) = \frac{x^2 - 1}{x - 1} \)

Réponse :

Explication: La fonction n'est pas définie en x = 1, mais elle peut être prolongée par continuité en ce point. En effet, \( \lim_{x \to 1} h(x) = 2 \). Donc, si on définit h(1) = 2, la fonction devient continue sur tout ℝ.

Déterminer si la fonction suivante est continue en x = 0 :

\( f(x) = \begin{cases} \sin(x)/x & \text{si } x \neq 0 \\ 1 & \text{si } x = 0 \end{cases} \)

La fonction est-elle continue en x = 0 ?

Explication: Cette fonction est continue en x = 0. En effet, \( \lim_{x \to 0} \frac{\sin(x)}{x} = 1 \), ce qui correspond à la valeur définie pour f(0).

La fonction exponentielle est-elle continue sur ℝ ?

\( g(x) = e^x \)

Réponse :

Explication: Oui, la fonction exponentielle est continue sur tout ℝ. Elle est dérivable (et donc continue) en tout point, et sa dérivée est elle-même continue.

Étude de la Continuité