1.3. Fonctions continues

Que signifie fonction continue ?

Tout le monde a une idée intuitive de la notion de continuité. On peut l’interpréter par le fait de ne jamais lever le crayon lorsqu’on dessine la courbe (graphique) d’un point à un autre. Essayons de l'exprimer analytiquement.

§1.3.1 Introduction

Définition

Soit une fonction \( f \) définie au voisinage de \(x=a \). On dit que \( f \) est continue au point \( x = a\) si et seulement si :

\( \lim_{(x \to a)} f(x) = f(a) \)

Cela signifie que :

  1. \( \lim_{(x \to a)} f(x) \)
  2. \( f(a) \)
  3. \( f(a) = L \)

Remarques

  1. Si l'une des deux limites \( L^- \) ou \( L^+ \) n'existe pas ou est infinie, il s'agit d'une discontinuité essentielle ou discontinuité de deuxième espèce. Par opposition, les discontinuités où les limites existent mais sont différentes sont regroupées sous le nom de discontinuité de première espèce. Il est important de noter que les discontinuités essentielles sont à distinguer des singularités essentielles en analyse complexe.

  2. Si une fonction possède une asymptote verticale en \(x = a\), alors \(\lim_{x \to a}\) est infinie.

  3. Et réciproquement ?

    Si \(f\) est continue au point \(x = a\), alors \(f\) possède une A.V. en \(x = a\) → Faux !

    Contre-exemple:

    Un exemple de fonction discontinue qui n'a pas d'asymptote verticale est :

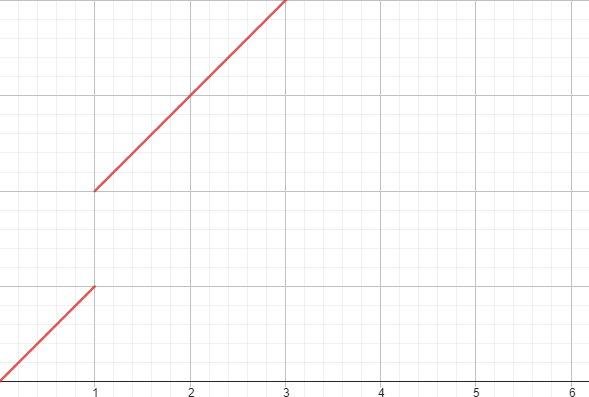
    $$ f(x) = \begin{cases} x^2 & \text{si } x < 2 \\ x-1 & \text{si } x \geq 2 \end{cases} $$

    Cette fonction est discontinue au point \(x=2\) car la limite de \(f(x)\) lorsque \(x\) tend vers \(2\) par la gauche n'est pas égale à \(f(2)\). Cependant, elle n'a pas d'asymptote verticale, car la fonction ne tend pas vers \(+\infty\) ou \(-\infty\) en approchant \(2\).

    4. En effet, \(\lim_{x \to 2^-} f(x) = 4\), tandis que \(f(2) = 1\).

    discontinue-sans-AV

  4. La notion de continuité est une notion locale. Néanmoins, on dira qu'une fonction \(f\) est continue sur un intervalle \(I = [a; b],\) si \(f\) est continue en chaque point de \(I = [a; b]\).

§1.3.2 Propriétés des fonctions continues

Soit \( f \) et \( g \) deux fonctions réelles continues en \( x = a \). Alors :

  1. \( \lambda \cdot f \) est continue en \( x = a \) pour tout \( \lambda \in \mathbb{R} \)
  2. \( f + g \) est continue en \( x = a \)
  3. \( f - g \) est continue en \( x = a \)
  4. \( f \cdot g \) est continue en \( x = a \)
  5. \( \frac{f}{g} \) est continue en \( x = a \), si \( g(a) \neq 0 \)
  6. Si \( f \) est continue en \( x = a \) et \( g \) est continue en \( y = f(a) \), alors \( g \circ f \) est continue en \( x = a \).

Exemples

Étudions la continuité des fonctions suivantes :

  1. \( h(x) = 3 \cdot \sqrt{x} \) est continue sur \( \mathbb{R}^+ \)
  2. \( h(x) = x^3 + \sqrt{x} \) est continue sur \( \mathbb{R}^+ \)
  3. \( h(x) = \frac{x^2}{x-1} \) est continue sur \( \mathbb{R} \setminus \{1\} \)

Ainsi, pour le point c) ci-dessus, on peut ajouter avec certitude qu'une fonction rationnelle est continue sur son domaine de définition, c'est-à-dire \( \mathbb{R} \setminus \) {valeurs interdites (zéro(s)) du dénominateur}.

Remarque

Les propriétés sur les fonctions continues nous permettent de déterminer si une fonction « compliquée » est continue en un point, en étudiant la continuité de chacune de ses parties en ce point, comme par exemple pour $$ h(x) = \frac{x^4 - 5x + 2}{\sqrt{x} - 1} $$.

\( D_h = \mathbb{R}^+ \setminus \{1\} \), donc \(h\) est continue sur \(\mathbb{R}^+ \setminus \{1\}\).

Démonstration

Par hypothèse, \( f \) et \( g \) sont deux fonctions continues en \( x = a \), c'est-à-dire :

\[ \lim_{(x \to a)} f(x) = f(a) \quad \text{et} \quad \lim_{(x \to a)} g(x) = g(a) \]

  1. \( \lim_{(x \to a)} (\lambda \cdot f)(x) = \lim_{(x \to a)} (\lambda \cdot f(x)) = \lambda \cdot \lim_{(x \to a)} f(x) = \lambda \cdot f(a) = (\lambda \cdot f)(a) \)
  2. \( \lim_{(x \to a)} (f + g)(x) = \lim_{(x \to a)} (f(x) + g(x)) = \lim_{(x \to a)} f(x) + \lim_{(x \to a)} g(x) = f(a) + g(a) = (f + g)(a) \)
  3. \( \lim_{(x \to a)} (f - g)(x) = \lim_{(x \to a)} (f(x) - g(x)) = \lim_{(x \to a)} f(x) - \lim_{(x \to a)} g(x) = f(a) - g(a) = (f - g)(a) \)
  4. \( \lim_{(x \to a)} (f \cdot g)(x) = \lim_{(x \to a)} (f(x) \cdot g(x)) = \lim_{(x \to a)} f(x) \cdot \lim_{(x \to a)} g(x) = f(a) \cdot g(a) = (f \cdot g)(a) \)
  5. \( \lim_{(x \to a)} \left(\frac{f}{g}\right)(x) = \lim_{(x \to a)} \left(\frac{f(x)}{g(x)}\right) = \frac{\lim_{(x \to a)} f(x)}{\lim_{(x \to a)} g(x)} = \frac{f(a)}{g(a)} = \left(\frac{f}{g}\right)(a) \)