1.4. Calcul différentiel
La notion de dérivée est le coeur du calcul différentiel. Voici l’approche géométrique de la notion de dérivée : On aimerait pouvoir connaître la pente de la droite tangente \(T\) en un point quelconque d’une courbe car elle nous permet de savoir comment se comporte la courbe en ce point (comportement local).
§1.4.1 Introduction (Approche géométrique de la notion de dérivée)
Soit \( f \) une fonction définie au voisinage de \( x_0 \). Prenons le point fixe \( (x_0, f(x_0)) \) sur le graphique de \( f \).
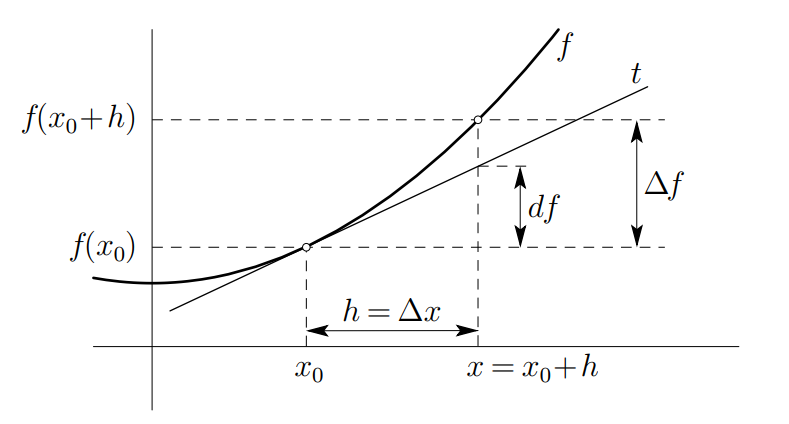
L'image montre une courbe représentant une fonction \( f \) et une tangente \( t \) à cette courbe en un point \( x_0 \). Voici les éléments clés illustrés :
- \( f(x_0) \) : la valeur de la fonction \( f \) en \( x_0 \).
- \( f(x_0 + h) \) : la valeur de la fonction \( f \) en \( x_0 + h \).
- \( h = \Delta x \) : l'intervalle entre \( x_0 \) et \( x_0 + h \).
- \( \Delta f \) : la différence entre \( f(x_0 + h) \) et \( f(x_0) \).
- \( df \) : la différence entre la valeur de la tangente \( t \) en \( x_0 + h \) et \( f(x_0) \).
Définition
Soit \( f \) une fonction définie au voisinage de \( x_0 \). Prenons le point fixe \( (x_0, f(x_0)) \) sur le graphique de \( f \). La dérivée de \( f \) en \( x_0 \) est la limite du rapport des différences finies \( \frac{\Delta f}{\Delta x} \) lorsque \( \Delta x \) tend vers zéro. Graphiquement, cela correspond à la pente de la tangente à la courbe de \( f \) en \( x_0 \).
L'image illustre comment la dérivée est géométriquement interprétée. La dérivée de \( f \) en \( x_0 \) est la limite du rapport des différences finies \( \frac{\Delta f}{\Delta x} \) lorsque \( \Delta x \) tend vers zéro. Graphiquement, cela correspond à la pente de la tangente à la courbe de \( f \) en \( x_0 \).
(i) Si une fonction \( f \) est dérivable en tout point d'un intervalle ouvert \( I = ]c; d[ \), on dit que \( f \) est dérivable sur \( I \).
(ii) Si \( f \) est dérivable sur \( I \), \(\text{la fonction dérivée de}\) \(f\) est :
\[ f' : I \to \mathbb{R} \]
\[ x \mapsto f'(x) \]
§1.4.2 Règles de dérivation
Le but de ce paragraphe est d’énoncer et de démontrer certaines formules qui permettent d’obtenir plus rapidement la dérivée de nombreuses fonctions sans passer par un calcul de limite.
a) $(3x^2-5x+7)'$
Solution :
On applique la règle de dérivation pour les polynômes :
$$(3x^2-5x+7)' = 6x-5$$
Explication :
- La dérivée de $3x^2$ est $6x$
- La dérivée de $-5x$ est $-5$
- La dérivée de 7 est 0
b) $\left(\frac{x^2}{2x+1}\right)'$
Solution :
On applique la règle du quotient :
\(\left(\frac{x^2}{2x+1}\right)' = \frac{(2x)(2x+1) - x^2(2)}{(2x+1)^2} = \frac{4x^2+2x-2x^2}{(2x+1)^2} = \frac{2x^2+2x}{(2x+1)^2}\)
Explication :
- On utilise la formule : $\left(\frac{u}{v}\right)' = \frac{u'v-uv'}{v^2}$
- Où $u = x^2$ et $v = 2x+1$
- $u' = 2x$ et $v' = 2$
c) $\left((3x^4-x^2)^7\right)'$
Solution :
On applique la règle de la chaîne :
$$\left((3x^4-x^2)^7\right)' = 7(3x^4-x^2)^6 \cdot (12x^3-2x)$$
Explication :
- On utilise la règle de la chaîne : $(f(g(x)))' = f'(g(x)) \cdot g'(x)$
- La dérivée de $3x^4$ est $12x^3$
- La dérivée de $-x^2$ est $-2x$
- On multiplie par 7 car c'est la dérivée de la puissance 7
Remarques
Il est possible d'obtenir ces dérivées avec la définition de la dérivée mais c'est beaucoup plus long et laborieux. Les règles de dérivation nous permettent de calculer plus efficacement.
Règles de dérivation
Soit \( f \) et \( g \) deux fonctions dérivables en \( x = a \), alors :