Limite d'une fonction

§1.1.1. Introduction et définition

Définition : Soit une fonction définie au voisinage de \( a \) (proche de \( a \), mais pas forcément en \( a \)). On dira que \( \lim_{x \to a} f(x) = L \) si pour des valeurs de \( x \) suffisamment proches de \( a \), mais différentes de \( a \), \( f(x) \) se rapproche aussi près qu'on veut de \( L \).

Cette expression se lit "la limite de \( x \) qui tend vers \( a \) de \( f(x) \) est égale à \( L \)".

Remarques :

\( \lim_{x \to a} f(x) = L \) ne veut pas dire que \( f(a) = L \).
La valeur de \( a \) ne doit pas nécessairement appartenir au domaine de définition de \( f \). Dans la majorité des cas, \( a \notin D_f \).
Il existe une définition mathématique plus formelle de la limite d'une fonction. Nous ne l'aborderons pas dans ce cours.

§1.1.2 Limites à gauche, limite à droite

Exemples :

Prenons la fonction :

\( f(x) = \begin{cases} x & \text{si } x < 1 \\ x+1 & \text{si } x=> 1 \end{cases} \)

On remarque :

Lorsque \( x \) se rapproche de \( 1 \) par des valeurs inférieures à \( 1 \) (par la gauche), \( f(x) \) se rapproche de \( 1 \). On note alors \( \lim_{x \to 1^-} f(x) = 1 \)
Lorsque \( x \) se rapproche de \( 1 \) par des valeurs supérieures à \( 1 \) (par la droite), \( f(x) \) se rapproche de \( 2 \). On note alors \( \lim_{x \to 1^+} f(x) = 2 \)

Qu'en est-il de la valeur \( \lim_{x \to 1} f(x) \) ? La limite n'existe pas !

Plus généralement

On dira que la limite existe si la limite à gauche vaut la limite à droite. Graphiquement, cela signifie que les deux «bouts» de la courbe arrivent au même point.

\( \lim_{x \to a^-} f(x) \) est la limite de \( f(x) \) lorsque \( x \) tend vers \( a \) par la gauche (par des valeurs inférieures à \( a \)).
\( \lim_{x \to a^+} f(x) \) est la limite de \( f(x) \) lorsque \( x \) tend vers \( a \) par la droite (par des valeurs supérieures à \( a \)).
\( \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) = L \iff \lim_{x \to a} f(x) = L \) (la limite existe)
\( \lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x) \iff \lim_{x \to a} f(x) \) n'existe pas

§1.1.2. Propriétés des limites

§1.1.3. Calculs des limites

Lorsqu'on calcule une limite, on peut obtenir :

un nombre réel ;
\( +\infty \) ou \( -\infty \) ;
une forme indéterminée telle que \( \frac{0}{0} \), \( \frac{\infty}{\infty} \), \( \infty - \infty \).

1. La limite est un nombre réel

Exemple : \( \lim_{x \to 3} (3x^2 - 7x - 1) = 3 \cdot 3^2 - 7 \cdot 3 - 1 = 27 - 21 - 1 = 5 \)

2. La limite est une forme \( +\infty \) ou \( -\infty \)

Exemples :

\( \lim_{x \to -\infty} (3x + 1) = 3 \cdot (-\infty) + 1 -> (négligeable) = -\infty \)

\( \lim_{x \to +\infty} (3x + 1) = +\infty \)

\( \lim_{x \to -\infty} (-3x + 1) = +\infty \)

\( \lim_{x \to -\infty} (\frac{x}{3} - 1) = -\infty \)

\( \lim_{x \to +\infty} (3x^2 - 1) = +\infty \)

\( \lim_{x \to -\infty} (-3x^2 - 1) = -\infty \)

3. La limite est une forme indéterminée

On dit qu'une limite est indéterminée si l'application des propriétés des limites ne permet pas de prévoir sa valeur. Dans ce cas, il faut avoir recours à des manipulations algébriques pour se ramener, si possible, à des cas déterminés. Les différents types d'indéterminations sont :

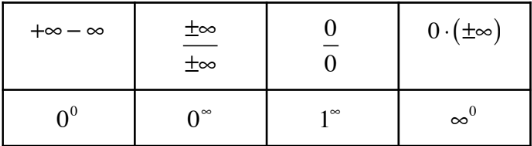
Voici quelques méthodes permettant de lever une indétermination, généralement symbolisée par des guillemets :

Factorisation dans le cas où l'indétermination est du type \( \frac{0}{0} \)

Exemples:

\( \lim_{x \to 3} \frac{x^2 - 9}{x - 3} = \frac{(3)^2 - 9}{3 - 3} = "\frac{0}{0}" \)

\( \lim_{x \to 1} \frac{x^2 + 3x + 2}{x^2 + 4x + 3} = \frac{1 + 3 + 3}{3 + 3} = \frac{1}{6} \)
\( \lim_{x \to -1} \frac{x^2 + 3x + 2}{x^2 + 4x + 3} = "\frac{0}{0}" \)

Mais aussi \( \lim_{x \to -1} \frac{x^2 + 3x + 2}{x^2 + 4x + 3} = \lim_{x \to -1} (\frac{\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x+3)}) \)

\( = -\frac{1+2}{-1+3} = \frac{1}{2} \)

Limite à gauche et à droite dans le cas où l'indétermination est du type \(\frac{\text{''nombre''}}{0}\)

Exemples:

\(\lim_{x \to 3} \frac{x - 7}{x^2 - 9}=\frac{3-7}{3^2-9}=\frac{-4}{0}\)

A gauche : \( \lim_{x \to 3^-} \frac{x-7}{x^2-9} = \frac{3-7}{(3^-)^2-9} = \frac{-4}{0^-} = +\infty \)

A droite : \( \lim_{x \to 3^+} \frac{x-7}{x^2-9} = \frac{3-7}{(3^+)^2-9} = \frac{-4}{0^+} = -\infty \)

Conclusion: \( \lim_{x \to 3} \frac{x - 7}{x^2 - 9} \notin \mathbb{R} \) et on peut dire que la fonction \( f(x)= \frac{x - 7}{x^2 - 9} \) admet une AV en x=3.
\( \lim_{x \to -1} \frac{x^2 - 3x + 2}{x^2 + 4x + 3}=\frac{(-1)^2 - 3(-1) + 2}{(-1)^2 + 4(-1) + 3}=\frac{1+3+2}{1-4+3}=\frac{6}{0} \)

A gauche : \( \lim_{x \to -1^-} \frac{x^2 - 3x + 2}{x^2 + 4x + 3} = \lim_{x \to -1^-} \frac{(x - 1)(x - 2)}{(x + 1)(x + 3)} = \frac{(-2)(-3)}{(0^-)(2)} = \frac{6}{0^-} = -\infty \)

A droite : \( \lim_{x \to -1^+} \frac{x^2 - 3x + 2}{x^2 + 4x + 3} = \lim_{x \to -1^+} \frac{(-2)(-3)}{(0^+)(2)} = \frac{6}{0^+} = +\infty \)

Conclusion: \( \lim_{x \to -1} \frac{x^2 - 3x + 2}{x^2 + 4x + 3} \notin \mathbb{R} \) et \( f(x)= \frac{x^2 - 3x + 2}{x^2 + 4x + 3} \) admet une AV en x=-1.

Mise en évidence forcée dans le cas où l'indétermination est du type \( +\infty - \infty \)

Exemples:

\( \lim_{x \to +\infty} (3x^2 - x + 1) = 3 \cdot (+\infty)^2 - \infty + 1 = +\infty - \infty \)

Mais aussi \( \lim_{x \to +\infty} (3x^2-x+1) = \lim_{x \to +\infty} x^2 \cdot (3 - \frac{1}{x} + \frac{1}{x^2}) = (+\infty)^2 \cdot (3 - \frac{0}{\infty} + \frac{0}{\infty^2}) = \infty \cdot 3 = +\infty \)
\( \lim_{x \to -\infty} (-7x^3 - 2x^2 + 4)= +\infty - \infty \)

Mais aussi \( \lim_{x \to -\infty} (-7x^3 - 2x^2 + 4) = \lim_{x \to -\infty} ( x^3 \cdot -7 - \frac{2}{x} + \frac{4}{x^3} ) = (-\infty)^3 \cdot (-7) = +\infty \)
\( \lim_{x \to -\infty} \frac{3x^3 + x^2 + 1}{x^2 + 3x} = \frac{-\infty + \infty}{\infty - \infty} \)

Mais aussi \( \lim_{x \to -\infty} \frac{3x^3 + x^2 + 1}{x^2 + 3x} = \lim_{x \to -\infty} \frac{x^3 \cdot (3 + \frac{1}{x} + \frac{1}{x^3})}{x^2 \cdot ( \frac{3}{x} + 1 )} = \frac{-\infty \cdot 3}{1} = -\infty \)

La fonction \( f(x) = \frac{3x^2 + 1}{x + 3} \) n'admet pas d'AH
\( \lim_{x \to +\infty} \frac{2x^4 + x^2 + 1}{x^4 + 1} = \frac{+\infty}{+\infty} \)

Mais aussi \( \lim_{x \to +\infty} \frac{2x^4 + x^2 + 1}{x^4 + 1} = \lim_{x \to +\infty} \frac{\cancel{x^4} \cdot (2 + \frac{x^2}{x^4} + \frac{1}{x^4})}{\cancel{x^4} \cdot (1 + \frac{1}{x^4})} = \frac{2}{1} = 2 \)

La fonction \( f(x) = \frac{2x^4 + x^2 + 1}{x^4 + 1} \) admet une AH en y = 2
\( \lim_{x \to -\infty} \frac{x^2 + 1}{x^3 - 1} = \frac{\infty}{-\infty} \)

Mais aussi \( \lim_{x \to -\infty} \frac{x^2 + 1}{x^3 - 1} = \lim_{x \to -\infty} \frac{x^2 \cdot (1 + \frac{1}{x^2})}{x^3 \cdot (1 - \frac{1}{x^3})} = \frac{1}{-\infty} = 0 \)

La fonction \( f(x)=\frac{x^2 + 1}{x^3 - 1} \) admet une AH en y = 0
\( \lim_{x \to +\infty} (x + \sqrt{x^2 - x}) = \infty + \sqrt{\infty^2 - \infty} = \infty + \sqrt{\infty} = \infty + \infty = \infty \)

\( \lim_{x \to +\infty} (x + \sqrt{x^2 (1 - \frac{1}{x})}) = \lim_{x \to +\infty} (x + \sqrt{x^2}) = \lim_{x \to +\infty} (x + x) = \lim_{x \to +\infty} 2x = +\infty \)

Proposition 1

Le comportement d'une fonction polynomiale à l'infini est le même que celui du terme de plus haut degré. On obtient ainsi \( \pm \infty \)

Exemple : \( \lim_{x \to -\infty} (-x^5 - x + 4) = \lim_{x \to -\infty} (x^5 \cdot (-1 - \frac{1}{x^4} + \frac{4}{x^5})) = \lim_{x \to -\infty} ((- \infty)^5 \cdot (-1 - \frac{1}{x^4} + \frac{4}{x^5})) = (-\infty) \cdot (-1) = +\infty \)

Proposition 2

Le comportement d'une fonction rationnelle à l'infini dépend du degré du numérateur et du dénominateur.

On distingue 3 cas:

(I) Si le degré du numérateur est supérieur à celui du dénominateur, on obtient \( \pm \infty \)

Exemple : \( \lim_{x \to -\infty} \frac{-x^5 - x + 4}{x - 1} = \lim_{x \to -\infty} \frac{x^5 (-1 - \frac{1}{x^4} + \frac{4}{x^5})}{x (1 - \frac{1}{x})} \)

\( = (-\infty)^4 \cdot (-1) = -\infty \)

Interprétation: la fonction \( f(x) = \frac{-x^5 - x + 4}{x - 1} \) n'admet pas d'asymptote horizontale. Admet-elle une asymptote oblique ?

(II) Si le degré du numérateur est égal à celui du dénominateur, on obtient un nombre réel différent de zéro.

Exemple : \( \lim_{x \to -\infty} \frac{2x^5 - x + 4}{x^5 - 1} = \lim_{x \to -\infty} \frac{x^5 (2 - \frac{1}{x^4} + \frac{4}{x^5})}{x^5 (1 - \frac{1}{x^5})} = \frac{2 - \frac{1}{(-\infty)^4} + \frac{4}{(-\infty)^5}}{(1 - \frac{1}{(-\infty)^5})} = \frac{2}{1} = 2 \)

Interprétation: la fonction \( g(x) = \frac{2x^5 - x + 4}{x^5 - 1} \) admet une asymptote horizontale en y=2.

(III) Si le degré du numérateur est inférieur à celui du dénominateur, on obtient 0.

Exemple : \( \lim_{x \to -\infty} \frac{2x^5 - x + 4}{x^6 - 1} = \lim_{x \to -\infty} \frac{x^5 (2 - \frac{1}{x^4} + \frac{4}{x^5})}{x^6 (1 - \frac{1}{x^6})} = \frac{2 - \frac{1}{(-\infty)^4} + \frac{4}{(-\infty)^5}}{-\infty \cdot (1 - \frac{1}{(-\infty)^6})} = \frac{2}{-\infty} = 0 \)

Interprétation: la fonction \( h(x) = \frac{2x^5 - x + 4}{x^6 - 1} \) admet une asymptote horizontale en y=0.